于佳曦[1]

内容提要：本文通过建立1985～2015年全国31个年份的时间序列模型，验证资源税与资源利用效率之间的关系，经过协整分析和平稳性检验，得出结论，增加资源税可以减少单位GDP原油消耗量、煤炭消耗量，说明资源税具有节约能源、提高资源利用效率的效果。因此，建议深化资源税改革，调整资源税征税目的，扩大资源税征税范围，合理确定资源税税率，完善资源税计税依据，通过税收促进资源的高效开发和集约利用。

关键词：资源税 资源利用效率 时间序列模型

对于资源税提高资源利用效率，有效实现节能的实证分析，国内外均有不同方向的研究。StefanGiljum、AmoBehrens（2007）等认为对自然资源课税（包括开采税、二氧化碳税等）可以影响资源产品的价格，进而影响经济发展，对自然资源课税可以实现自然资源的可持续发展。Markandya（2009）通过分析欧盟内部不同国家在节能电器产品生产、消费中所采用的税率，认为可以通过实行能源资源差别税率提高能源利用效率。Conrad（2009）认为对能源征税间接地提高了能源价格，加大了消费者的能源使用成本。同时，市场竞争压力会促使汽车生产者研究开发出更节能的汽车，减少消费者使用成本，提高能源利用效率。Allcott（2014）等研究了能源的政策效应，结果表明对能源征税，可以有效推动社会对提高能源利用率方面的投资，并减少能源消耗带来的外部性。

国内学者不乏对资源税节能效果的相关研究。比如，金成晓、张东敏（2015）研究油气资源税从价计征改革的政策效应，运用双重差分法分析了油气资源税从价计征改革与单位产值能耗等指标之间的关系，结果表明油气资源税从价计征促进了资源利用效率的提高。李一花、丌艳萍（2016）则运用1994～2013年的资源税数据，利用时间序列模型进行实证分析，结果表明，在长期内资源税与原油开采量之间呈负相关关系，但资源税从价计征改革削弱了这种关系。2014年，煤炭继油气之后，开始采用“从价计征”方式。徐晓亮、程倩等（2015）通过构建动态递归可计算一般均衡模型，发现以2%、5%和10%作为煤炭资源税的从价税率区间时，资源税从价计征能降低单位GDP能耗。刘宇、周梅芳（2015）同样运用可计算一般均衡模型研究煤炭资源税政策效应，与徐晓亮等不同，这一研究假定了有、无税收返还两种情形，认为存在税收返还的情况下，从价计征资源税更能促进能源和资源的节约。

纵观以往的实证研究，或时间序列样本时间年限过短，或缺少对多种能源进行资源税的节能效果检验，本节修正上述不足，利用我国1985～2015年共计31年的时间序列数据，检验我国资源税与单位GDP主要资源（石油、煤炭、天然气）消耗量之间，是否具有长期均衡关系（即协整关系）。如果长期均衡关系成立，并且是负的关系，则说明征收资源税能够提高资源利用效率。

一、变量及数据说明

本文选取了我国“单位GDP煤炭消耗量（y₁）”、“单位GDP石油消耗量（y₂）”和“单位GDP天然气消耗量（y₃）”三个指标来反映资源利用效率；选取了“资源税额（x₁）”作为资源税征收指标；选取了 “工业产值占GDP的比重（x₂）”作为控制变量，分别建立了三个系统的时间序列模型。其中，由三维变量y₁、x₁和x₂构成的系统，本文以下称为“系统1”；由三维变量y₂、x₁和x₂构成的系统，本文以下称为“系统2”；由三维变量y₃、x₁和x₂构成的系统，本文以下称为“系统3”。所有变量的样本数据均为时间序列，样本期间为1985～2015年，共31年的观测值。数据分别来源于1985～2015年《中国统计年鉴》、《中国税务年鉴》、《中国经济年鉴》及中国经济社会发展数据统计网站。所选取变量的详细情况见表1，表中各变量单位的选择是为了避免各变量间的数量级差过于悬殊，出现计算机运算的较大误差。

二、变量描述性统计分析

本文通过绘制所选变量的时间趋势图，更加直观地描述“单位GDP煤炭消耗量y₁”、“单位GDP石油消耗量y₂”、“单位GDP天然气消耗量y₃”、“资源税额x₁”和“工业产值占GDP的比重x₂”在样本期间内的变化趋势（见图1）。

图1 五个变量样本期间的变化趋势

从图1可以看出，变量y₁、y₂、y₃在样本期间一直呈下降趋势，说明这三种资源的利用效率在不断提高；变量x₁在样本期间一直呈上升趋势，说明资源税的征收力度在不断加大（这与我国资源税的改革方向相吻合）；变量x₂在样本期间总体呈上升趋势，说明在样本期间我国第二产业的比重在不断增加。总之，变量y₁、y₂、y₃的下降趋势以及变量x₁的上升趋势表明，三种资源的利用效率与资源税额之间呈现出较为明显的负相关趋势。

本文进一步计算了五个变量间的简单样本相关系数，验证三种资源的利用效率与资源税额之间的负相关关系（见表2）。表2中，变量x₁分别与变量y₁、y₂在5%显著性水平下呈显著负相关；而变量x₁与变量y₃虽然在5%显著性水平下不显著相关，但在10%显著性水平下呈显著负相关。

注：“P值”是指检验原假设“总体相关系数为0”时，检验统计值对应的双侧概率；“*”表示在5%显著性水平下，拒绝了“总体相关系数为0”的原假设。

通过以上对图1及表2的综合分析可以确认，从样本数据上看，变量x₁分别与变量y₁、y₂和y₃之间存在负的相关关系，即随着资源税征收力度的加大，各种资源利用效率在提高。但是这种负的相关关系只是根据样本数据得来，不能确定其是由于样本数据的偶然性造成的，还是确实存在长期的负均衡关系（即协整关系），还需进一步建立相关模型加以实证分析。

三、资源税对资源利用效率影响的实证分析

所有相关变量都具有相同的单整阶数，是这些变量间存在协整关系的前提条件。如果各变量都具有相同单整阶数，说明它们之间可能存在协整关系，可以进一步通过协整检验确定是否存在协整关系；如果各变量单整阶数不同，说明它们之间不可能存在协整关系。因此，验证征收资源税是否影响资源利用效率，即在控制了相关协变量x₂的情况下，变量x₁分别与变量y₁、y₂和y₃之间是否存在长期均衡的负相关关系，就需要检验变量x₁分别与变量y₁、y₂和y₃之间是否存在协整关系，如果具有协整关系，则说明存在长期均衡关系，否则不存在长期均衡关系。

（一）各变量单整阶数的确定

1. 检验各变量的水平值之间是否存在单位根

为确定各变量的单整阶数，首先对各个变量的水平值进行ADF单位根检验。利用STATA软件，对单位GDP煤炭消耗量y₁、单位GDP石油消耗量y₂、单位GDP天然气消耗量y₃、资源税税额x₁、第二产业比重x₂，五个变量的水平值进行单位根检验。结果见表3。

注：“c”代表ADF检验方程中含有常数项，“t”代表ADF检验方程中含有时间趋势项，是否含有常数项和时间趋势项是通过绘制各变量时间趋势图以及显著性t检验确定的。“滞后阶数”表示ADF检验方程中自回归部分的滞后阶数，滞后阶数的确定方法是：首先运用公式P*=[12*(T/100)^(1/4)]计算最大滞后阶数,然后运用从大到小序贯t规则进行检验，直到在5%的显著性水平下滞后差分项的系数通过显著性检验为止。

如表3所示，5个变量检验统计值的绝对值均较小，对应的P值都大于5%，说明在5%的显著性水平下，对于所有变量均接受具有单位根的原假设，表明这五个变量均至少具有一个单位根。

2. 检验各变量的一阶差分是否存在单位根

通过上述检验，确定了各变量的水平值均存在单位根，即各变量至少是一阶单整过程，因此，需要进一步检验各变量是否是二阶单整过程，即对各变量的一阶差分进行单位根检验。单位GDP煤炭消耗量y₁、单位GDP石油消耗量y₂、单位GDP天然气消耗量y₃、资源税税额x₁、第二产业比重x₂五个变量一阶差分的ADF单位根检验结果见表4。

注：“c”、“t”和“滞后阶数”的含义及确定方法均与表3相同。

如表4所示，y₁、y₂、x₁和x₂四个变量的ADF检验统计值都小于相应的5%显著性水平下的临界值，而y₃在10%的显著性水平下拒绝“有单位根”的原假设。因此，总体上可以认为所有变量的一阶差分均不含单位根，为平稳的I(0)过程。

综合表3和表4的结果，可以确定以上5个变量均为一阶单整过程，即I（1）过程，因此，5个变量之间有可能存在协整关系。

（二）协整检验

为了进一步验证5个变量之间是否存在协整关系，需要确定相关系统的协整秩。如果协整秩为0，则相关系统变量间不存在协整关系；如果协整秩大于0，则相关系统变量间至少存在1个协整关系。本文分别对“由y₁、x₁和x₂构成的系统1”、“由y₂、x₁和x₂构成的系统2”和“由y₃、x₁和x₂构成的系统3”进行协整检验，检验方法是Johansen的迹检验，检验结果见表5。

注：“*”表示在5%显著性水平下选择的协整秩。

如表5所示，系统1和系统3的协整秩都为1，即各有一个协整向量，表明在变量y₁、x₁、x₂之间，以及变量y₃、x₁、x₂之间均各具有一个长期均衡关系。而系统2的协整秩为0，即没有协整向量，说明变量y₂、x₁、x₂之间没有长期均衡关系。

（三）VECM模型滞后阶数的选择

上述协整检验确认了系统1及系统3的变量间各存在一个协整关系，进一步通过估计这两个系统的向量误差修正模型（以下称“VECM模型”），来确定协整方程的系数，进而判断资源税对提高资源利用效率的效果。为了估计VECM模型，需要计算VECM模型的最大滞后阶数，其计算公式为P*=[12*(T/100)^(1/4)]，将本文的样本观测值数T=31代入公式中，计算得到P*=8.9，取P*=9。在此基础上，通过计算信息准则，系统1和系统3的VECM模型的最佳滞后阶数选择结果分别见表6和表7。

表6 系统1的最佳滞后期（信息准则标准）

注： “lag”表示原始VAR模型的滞后阶数；“LR”表示似然比统计值；“df”表示似然比统计量的自由度；“p”表示LR检验统计量对应的P值；“FPE”表示Akaike’s Final Prediction Error，度量向前一期预测的均方误差；“AIC”、“HQIC”、“SBIC”分别表示三个信息准则；“*”表示选择的最佳滞后阶数；“—”表示样本量不够大导致出现的缺失值（下同）。

注：同表6。

如表6、表7所示，根据FPE统计量，需要滞后6阶；根据LR统计量、AIC准则、HQIC准则、SBIC准则，需滞后8阶或9阶。虽然根据这些统计量，都应该选择较长的滞后阶数，但由于每个系统中包含了3个变量，滞后阶数的增加，会迅速减少系统的自由度。本文中每增加一个滞后阶数，会减少10个自由度，即“1(损失一个观测值)+3（变量的个数）*3（方程的个数）=10”。

本文所获得的样本观测值个数只有31个，不应选择过长的滞后阶数。考虑到增加滞后项的主要目的是为了消除误差项的序列相关，因此，本文尝试以VECM模型的“误差项不存在序列相关”为标准来确定滞后阶数。按照此标准，从滞后1阶开始估计VECM模型，并对其误差项是否存在序列相关进行检验，然后逐渐增加滞后阶数，直到两个系统的误差项均不存在序列相关为止，此时的滞后阶数即为最佳滞后阶数。按照“误差项不存在序列相关”标准，各系统的VECM模型的最佳滞后阶数选择结果见表8。

如表8所示，按照“误差项不存在序列相关”标准，对于系统1，在选择滞后阶数为“一阶”时，由于相应的P值分别为0.055和0.659，因此在10%显著性水平下拒绝了“误差项不存在1阶自相关”，并且在通常的显著性水平下接受了“误差项不存在2阶自相关”的原假设。因为误差项仍存在1阶自相关，说明滞后一阶的VECM模型过于简单，使得误差项仍然存在自相关。而在选择滞后阶数为“二阶”时，由于相应的P值分别为0.270和0.574，因此在5%显著性水平下分别接受了“误差项不存在1阶自相关”和“误差项不存在2阶自相关”的原假设，说明滞后二阶的VECM模型已经比较充分，误差项不存在自相关，因此对于系统1的VECM模型的最佳滞后阶数为2阶。同理，按照“误差项不存在序列相关”标准，系统2 的最佳滞后阶数也为2阶。

综上所述，根据信息准则，选择VECM模型的最佳滞后阶数为6阶或8阶，而根据“误差项没有自相关的标准”选择的VECM模型的最佳滞后阶数为2阶。作为折中，本文选择VECM模型的滞后阶数为4阶。

（四）估计误差修正模型（VECM）

由于系统2各变量间不存在协整关系，因此本文只对系统1和系统3进行误差修正模型（VECM）估计，在上文确定的系统1和系统3的滞后阶数以及协整秩的基础上，得到的系统1和系统3的VECM模型的MLE估计结果（见表9及表10）。

根据表9和表10的估计结果，可以写出系统1和系统3的协整方程，分别为

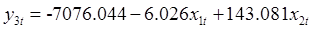
由于在系统1和系统3的协整方程中，资源税变量x₁的系数估计值均为负，且在1%的显著性水平下通过显著性检验，说明资源税对提高煤炭和天然气的利用效率具有促进作用。由于系统2没有协整关系，可以认为资源税对石油的利用效率没有影响。

在估计完误差修正模型后，为了验证模型估计结果的可信性，还需对模型的误差自相关进行诊断性检验。对系统1和系统3的VECM模型误差项是否存在自相关的检验结果见表11。由表11可以看出，对于两个系统的VECM模型，在5%的显著性水平下，均接受了“误差项不存在1阶及2阶自相关”的原假设，说明这两个系统的VECM模型较充分，估计结果具有可信性。

(五)VAR模型变量次序的确定

通过前文误差修正模型的估计，已经确认了征收资源税与资源利用效率之间存在长期的负均衡关系。在此基础上，为了进一步考察征收资源税对资源利用效率的影响，本文分别对系统1和系统3估计了正交脉冲响应函数（IRF）。由于正交脉冲响应函数的估计过程中，涉及到对VECM模型的残差协方差矩阵进行乔利斯基分解（Cholesky decomposition）,而乔利斯基分解的结果与系统中各变量的次序有关。因此，为了正确地估计正交脉冲响应函数，需要确定最佳的变量排序，本文选择的确定变量排序的方法是绘制各变量的交叉相关图（见图2）。

由图2（a）可以看出，交叉相关系数的绝对值的最大值在0的右边，可以视为变量y₁的当期变化会导致变量x₁的未来变化，因此变量y₁的次序应在变量x₁之前，记为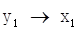。同理，由图2(b)(c)(d)(e)可知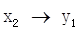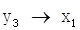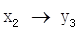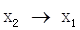：，，，。综合这些次序，可以得出系统1的变量顺序为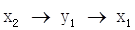，系统3的变量次序为。

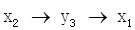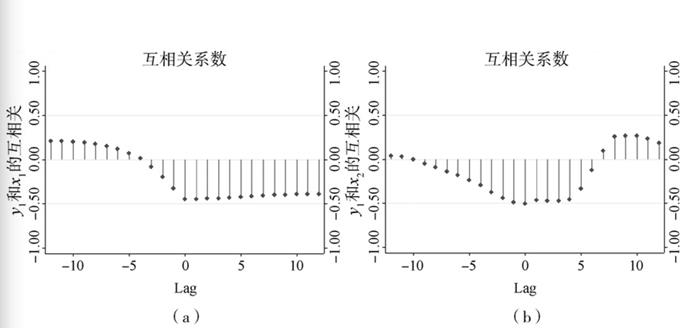
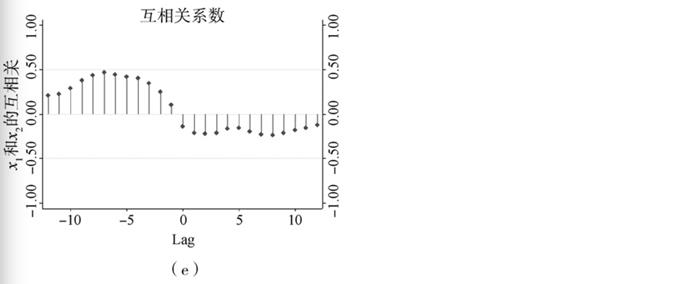
图2各变量之间的交叉相关分析

(六)正交脉冲响应函数分析

根据上文得到的的变量次序，分别估计系统1和系统3的VAR模型，然后计算相应的正交脉冲响应函数，绘制正交脉冲响应函数图，结果见图3和图4。

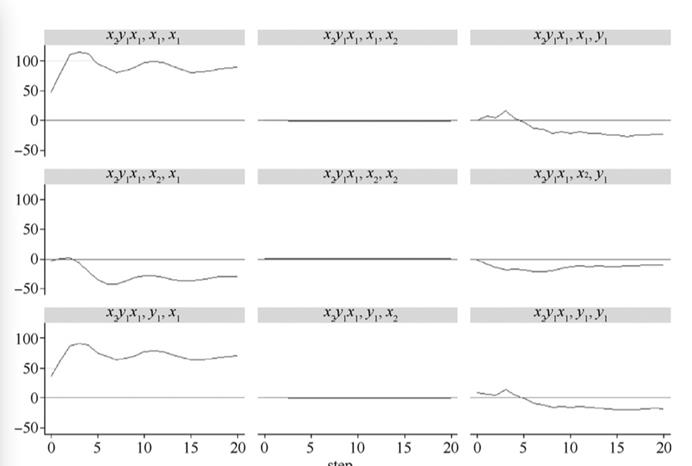
图3 系统1的正交脉冲响应函数（变量次序x₂→y1→x1）

注: 图中公式或变量依次表示脉冲响应函数、 脉冲变量、 响应变量。如 x2 y1 x1 表示 x2 与y1、 x1 的脉冲响应函数， x2y1x1，x1，x1 表示在脉冲响应函数x2y1x1 下， 对x1 施加脉冲，x1 的反应。x2y1x1， x1， x2 等以此类推。下同。

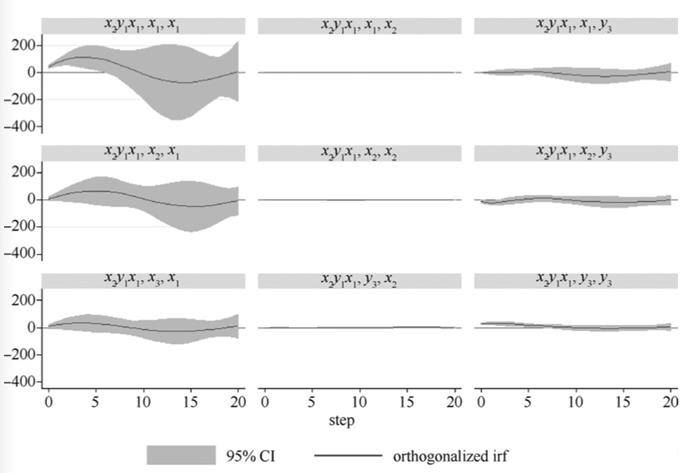
图4 系统3的正交脉冲响应函数（变量次序x₂→y₃→x₁）

由图3中第一行第三列的图可知， x₁一个单位（或一个标准差）的脉冲会引起y₁的持续下降。

由图4中第一行第三列的图可知， x₁一个单位（或一个标准差）的脉冲会引起y₃的持续下降，但降幅较小。

四、研究结论与建议

（一）结论

本文通过建立时间序列模型，验证资源税与资源利用效率之间的关系，经过协整分析和平稳性检验，得出增加资源税可以减少单位GDP原油、单位GDP煤炭消耗量。具体结论如下：

1. 通过对 y₁、y₂、y₃、x₁、x₂ 五个变量的描述性统计分析，确认了资源税征收额 (x₁ ) 和资源利用效率 (y₁ 、y₂ 、y₃ ) 之间存在负相关关系。

2. 通过对y1、 y2、 y3、 x1、 x2 五个变量水平值和一阶差分值的ADF 单位根检验，确定这五个变量都是一阶单整过程，说明五个变量之间具备存在协整关系的可能性。

3. 通过分别对系统1 (y1 和x1、 x2 之间)、 系统2 (y2 和x1、 x2 之间) 和系统3 (y3 和x1、x2) 变量之间进行协整检验，发现y1 和 x1、 x2 之间， y3 和 x1、 x2 之间各存在一个协整关系，y2 和 x1、 x2 之间不存在协整关系。说明 “单位 GDP 资源税额 x1 ” 对 “单位 GDP 煤炭消耗量 y1 ” 和 “单位 GDP 天然气消耗量 y3 ”具有长期影响，而对 “单位GDP原油消耗量y2” 没有长期影响。

4. 利用 “信息准则” 和 “误差项不存在序列相关” 两个标准，折中地对系统1和系统3 的VECM 模型滞后阶数进行了选择，综合确定了两个系统的VECM模型的最佳滞后阶数均为 4阶。

5. 通过估计系统1以及系统3的误差修正模型，得到两个协整方程。据此得出 x1 分别和 y1 、y3 之间具有长期的负的均衡关系，说明资源税额的增加会引起单位 GDP煤炭消耗量以及单位 GDP天然气消耗量的减少。

6. 通过确定系统1和系统3的VAR模型变量次序的，得知系统1的变量次序为x2→y1→x1，系统3的变量次序为x2→y3→x1。

7. 通过分析正交脉冲响应函数，进一步验证了 x1 与 y1 、y3 之间具有反向相关关系，即再次验证了增加资源税可以降低单位GDP煤炭、单位GDP天然气消耗量。

 （二）建议

上述实证研究表明，征收资源税有利于提高资源利用效率，节约资源。因此，为充分发挥资源税的调控作用，可在资源税的立法目的、征收范围、税率、计税依据等方面进行完善。

1. 改革资源税的立法目的

长期以来，我国资源税以调整级差收入、实现公平竞争为目标。在此目标下，资源税的制度设计偏向收入环节，而忽视了开采环节，导致资源开采企业即使存在过度开采和资源浪费的情形。当前我国的矿产资源存在着明显的过度开采问题，具有严重的负外部性,很大程度上影响了矿产资源及矿区的可持续利用和发展。在此背景下，应将资源税立法目的从“级差调节”转变为“节约资源”，在制度设计上，不仅充分体现资源的自身价值和作用，而且要实现资源开采的外部成本内部化。通过资源税有效协调人与环境、人与资源的关系，促进资源的高效开发、集约利用，实现可持续发展的税制改革目标。

2. 扩大资源税的征税范围

围绕“节约资源、保护环境”的制度目标，资源税的征收范围应当包括一切可开发和利用的国有资源，而我国现行的《中华人民共和国资源税暂行条例》以及《中华人民共和国资源税法（征求意见稿）》规定的征税范围只包括具有商品属性（价值和使用价值）的矿产品和盐两大类。综观许多发达国家，其资源税的征收范围已经包括了水、草原、森林等自然资源的使用。2016年7 月1 日，我国将水资源纳入了资源税的改革试点，并提出要“积极创造条件，逐步对水、森林、草场、滩涂等自然资源开征资源税”。[2]继续扩充资源税的征收范围已经成为下一步资源税改革的共识。一方面，要按照循序渐进的原则，分阶段将资源税扩围至森林、草原、滩涂等诸多自然资源，推进资源税征收范围的完善；另一方面，结合清费立税，逐步理顺税费关系。我国资源税费领域存在税费重叠、功能交叉的问题，例如，我国当前的政府性基金收费中包含了大量的国家资源使用费，名为草原植被恢复费、森林植被恢复费、探矿权采矿权使用费等，征收极为不规范。因此，可以结合政府性基金改革，取缔违规、越权设立的各项收费基金。另外，为了突出环境保护功能，有必要对我国现行的资源税税目进行细化调整，比如，煤炭资源的开采成本受到储藏条件、开采设施、产地煤级等方面的影响，开采成本差异较大，有必要进一步完善税目分类。

3.合理确定资源税的税率

本文实证研究表明，提高资源税税额可以有效降低单位GDP能源消耗。我国2016年实行的从价计征的资源税改革在一定程度上提高了资源税的税收收入，但是资源开采企业的整体税负仍然不高。提高资源税的税率标准，仍然要围绕资源可持续发展目标，综合考虑自然条件、资源丰度、开采阶段、交通状况、储藏条件，以及资源的可再生条件和可替代性等诸多因素，并按照资源消耗程度实行差别浮动税率。[3]

在确定资源税的税率差异方面，可以考虑将新开发或容易开发的资源采用高税率，以限制资源的过度开采和促进集约利用；而对开采难度较大的资源采用低税率，甚至给予优惠补贴，鼓励企业积极开采；在测算资源税有效税率方面，以可持续价值和环境损害成本为参考；在测度资源可持续增长价值方面，使用未来的重置成本估算，或采用可替代技术的净值，根据一定的贴现率在损耗年度内进行贴现；环境损害程度的测度，可以采用意愿调查法、生产函数法、离散选择价值评估法等进行评估。此外，资源税税率改革还应考虑企业的负担能力。

4.完善资源税的计税依据

我国资源税的计税依据并未放在开采环节，而是以“从量计征”的方式放于销售和使用环节。2016年我国资源税实行从价计征改革，虽然能够在一定程度上反映资源市场价值的变化，但并未改变计税依据的设定环节。企业不需要在开采环节付出税收代价，势必难以抑制盲目开采行为。因此，建议按照资源的回采率计征资源税。以回采率作为参考系数，如税额=储量×税率×回采（开采）率系数，可以有效促进开采和回采率，减少资源积压和存货损失。但按开采率计征资源税，需要解决可能面临的资源勘查、评估和预测水平等诸多技术和操作层面的问题。

参考文献：

[1]金成晓, 张东敏, 王静敏. 我国油气资源税由从量计征改为从价计征的政策效应——基于双重差分法的计量分析[J]. 财经理论与实践, 2015(5):91-96.

[2]李一花, 丌艳萍. 资源税改革的经济效应分析[J]. 山东工商学院学报, 2016(1):89-104.

[3]刘宇, 周梅芳. 煤炭资源税改革对中国的经济影响——基于 CGE 模型的测算[J], 宏观经济研究, 2015(2):60-67.

1. 徐晓亮, 程倩, 车莹, 许学分. 煤炭资源税改革对行业发展和节能减排的影响[J]. 中国人口·资源与环境, 2015(8):77-83.

   [5] Allcott H, Mullainathan S, Taubinsky D. Energy policy with externalities and internalities[J]. Journal of Public Economics, Vol. 112, April 2014:pp.72-78.

   [6] Conrad K. Energy Tax and Competition in Energy Efficiency: The Case of Consumer Durables[J]. Environmental and Resource Economics, Vol. 15, No. 2, February 2000:pp. 159–177.

   [7] Markandya A, Ortiz R A, Mudgal S, et al. .Analysis of tax incentives for energy-efficient durables in the EU[J]. Energy Policy, Vol. 37, No. 12, December 2009: pp. 5662-5674.

   [8] Stefan Giljum，Amo Behrens，Friedrich Hinterberger，et al. .Modelling Scenarios  towards A Sustainable Use of Natural Resources in Europe[J]，Environmental Science & Policy，Vol. 11, No. 3, May 2008: pp. 204-216.

   (作者单位:上海立信会计金融学院)

本文已收入《中国税收教育研究报告（2020）》